Skip to section navigation Skip to main content

Which Model Makes Sense?

Home > Which Model Makes Sense? > Page 5

Resources for this lesson:

> Glossary opens in new window
> Calculator Resources opens in new window
> Teacher Resources: Instructional Notes opens in new window

Did you confirm that a linear model was the best fit for the data?  Compare your response with the solution below:

Velocity of Projectile vs. Time

Time (seconds)

0

0.5

1

1.5

2

2.5

3

Velocity (feet per second)

49

34

19

2.5

−14

−30.5

−45

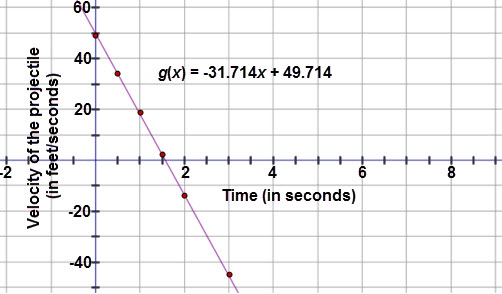
This graph is a scatter plot displaying the velocity of the projectile (in feet per second) for times 0 to 3 seconds. The horizontal axis extends from negative 2 to 9. The vertical axis extends from negative 50 to 60. The graph displays the following ordered pairs: (0, 49), (0.5, 34), (1, 19), (1.5, 2.5), (2, negative 14), and (3, negative 45). A line of best fit is drawn through the scatter plot, modeled with the linear regression equation g of x = negative 31.714x +49.714.

 

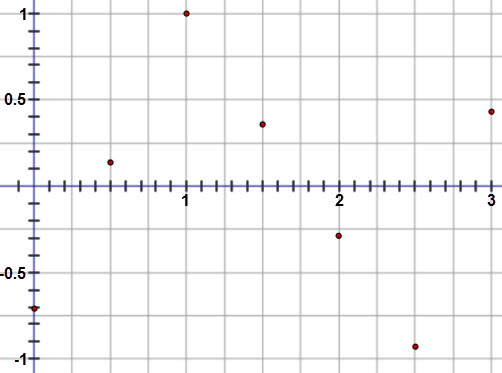
This graph is a residual plot show the residuals for times 0 to 3 seconds. The horizontal axis represents the time (in seconds) and extends from 0 to 3. The vertical axis represents the residuals when a linear modeled is applied to the data and extends from negative 1 to 1. The graph displays the following ordered pairs: (0, negative 0.71), (0.5, 0.14), (1, 1), (1.5, 0.36), (2, negative 0.29), (2.5, negative 0.93) and (3, 0.43).

The graph of the linear regression equation fits the scatter plot very well. The residuals are all fairly small and the graph of the residuals is random. The correlation coefficient when rounded to the nearest thousandth was negative 1, which indicates that there is a strong negative linear correlation between the variables. All of these facts indicate that a linear model is appropriate for the velocity versus time data.

 

< PreviousNext >