Student Resources
Glossary
Experimental probability: The ratio of the number of times the event occurs to the total number of trials.
Theoretical probability: The likelihood of an event happening based on all the possible outcomes. The ratio for the probability of an event 'P' occurring is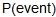 
= number of favorable outcomes divided by number of possible outcomes.
Sample space: In a probability model for a random process, a list of the individual outcomes that are to be considered.
Independent: When the outcome of one event does not influence the outcome of a second event. To find the probability of two independent events both occurring, multiply the probability of the first event by the probability of the second event.
Dependent: When the outcome of one event affects the outcome of a second event. To find the probability of two dependent events both occurring, multiply the probability of A and the probability of B after A occurs.
Mutually exclusive (disjoint): When two events cannot happen at the same time. To find the probability of one or the other of two mutually exclusive events, add the probability of the first event to the probability of the second event.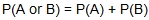 
.
Mutually inclusive: When two events can happen at the same time. To find the probability of one or the other of two mutually inclusive events, apply the Addition Rule.
Intersection: The case that both events A and B occur. Represented as 
or 
.
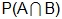Union: The case that either events A or B occur or both events occur. Represented as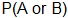 
or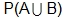 
.
Complement: The case that an event does not occur. Represented as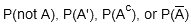
.
Addition Rule: To calculate 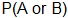for mutually inclusive events, add the probability of the first event to the probability of the second event and then subtract the probability of both occurring. 
.
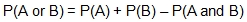Two-way table: A two-way table organizes data gathered measured by two categorical variables. Values of the row variable label the rows that run across the table, and values of the column variable label the columns that run down the table.
