Prize Winner, Part 3

Home > Prize Winner, Part 3 > Page 2

Khalid, Justyce, Andrew, Marissa and Allyson are satisfied with the game. They feel that the probabilities involved in the game make the game challenging, yet contestants do have a chance to win. They decide, based on the probabilities, to award three levels of prizes. They make the following rule sign to accompany the game board.

From your work above, you already know the following:

Prize	Probability to Win
Small	${\displaystyle \frac{12}{27}}$
Medium	${\displaystyle \frac{6}{27}}$
Large	${\displaystyle \frac{1}{27}}$

Recall how the game is created and conducted. Khalid, Justyce, Andrew, Marissa and Allyson designed the board so that one of three letters, A – B – C, is placed behind each of the doors. The letters are changed with each contestant to keep the game fair, and the letters behind the doors can repeat. For example, in one round the letter sequence could be C – B – A, and in the next round the letter sequence could be A – A – A.

How would the probabilities for the prizes change, if the letters behind the doors could not repeat?

Show AnswerHide Answer

It is important to understand that if the letters can't repeat, once you know the first two doors, right or wrong, you know the third door.
For a Small Prize:
= = ${\displaystyle \frac{2}{3}•\frac{1}{2}=\frac{1}{3}}$
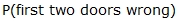For a Medium Prize: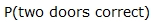
= or
= ${\displaystyle (\frac{2}{3}+\frac{1}{2})+(\frac{1}{3}+\frac{1}{2})=\frac{1}{2}}$
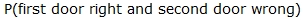
For a Large Prize: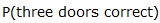
= = ${\displaystyle \frac{1}{3}•\frac{1}{2}=\frac{1}{6}}$

If the letters behind the doors do not repeat, it is clear that a person playing the game would stand a much better chance of winning a prize. Khalid, Justyce, Andrew, Marissa and Allyson do want people to stand a chance of winning but they do not want to make it too easy to win. They are concerned that if the letters cannot repeat that too many people will win and they will run out of prizes. If they keep the rule that the letters behind the doors cannot repeat, what other adjustment to the game could be made to make it a little harder to win a prize?

Show AnswerHide Answer

Answers may vary; possible answer: have four letters but three doors.

< Previous Next >