Teacher Resources
Prize Winner, Part 3
On this page you will find lesson objectives, standards, instructional notes and UDL opportunities.
Estimated Time: 90 minutes
Lesson Objectives:
- The students will apply their knowledge of probability to make informed decisions.
- The students will compute and interpret theoretical and experimental probabilities.
Key Common Core State Standards:
S.CP.1: Describe events as subsets of a sample space (the set of outcomes) using characteristics (or categories) of the outcomes, or as unions, intersections, or complements of other events (“or,” “and,” “not”).
S.CP.2: Understand that two events A and B are independent if the probability of A and B occurring together is the product of their probabilities, and use this characterization to determine if they are independent.
S.CP.3: Understand the conditional probability of A given B as P(A and B)/P(B), and interpret independence of A and B as saying that the conditional probability of A given B is the same as the probability of A, and the conditional probability of B given A is the same as the probability of B.
S.CP.4: Construct and interpret two-way frequency tables of data when two categories are associated with each object being classified. Use the two-way table as a sample space to decide if events are independent and to approximate conditional probabilities. For example, collect data from a random sample of students in your school on their favorite subject among math, science, and English. Estimate the probability that a randomly selected student from your school will favor science given that the student is in tenth grade. Do the same for other subjects and compare the results.
S.CP.5: Recognize and explain the concepts of conditional probability and independence in everyday language and everyday situations. For example, compare the chance of having lung cancer if you are a smoker with the chance of being a smoker if you have lung cancer.
S.CP.6: Find the conditional probability of A given B as the fraction of B’s outcomes that also belong to A, and interpret the answer in terms of the model.
S.CP.7: Apply the Addition Rule, P(A or B) = P(A) + P(B) – P(A and B), and interpret the answer in terms of the model.
Supporting Common Core State Standards:
7.SP.C.5: Understand that the probability of a chance event is a number between 0 and 1 that expresses the likelihood of the event occurring. Larger numbers indicate greater likelihood. A probability near 0 indicates an unlikely event, a probability around 1/2 indicates an event that is neither unlikely nor likely, and a probability near 1 indicates a likely event.
7.SP.C.6: Approximate the probability of a chance event by collecting data on the chance process that produces it and observing its long-run relative frequency, and predict the approximate relative frequency given the probability. For example, when rolling a number cube 600 times, predict that a 3 or 6 would be rolled roughly 200 times, but probably not exactly 200 times.
7.SP.C.7: Develop a probability model and use it to find probabilities of events. Compare probabilities from a model to observed frequencies; if the agreement is not good, explain possible sources of the discrepancy.
7.SP.C.8: Find probabilities of compound events using organized lists, tables, tree diagrams, and simulation.
7.SP.C.8a: Understand that, just as with simple events, the probability of a compound event is the fraction of outcomes in the sample space for which the compound event occurs.
7.SP.C.8b: Represent sample spaces for compound events using methods such as organized lists, tables and tree diagrams. For an event described in everyday language (e.g., “rolling double sixes”), identify the outcomes in the sample space which compose the event.
8.SP.4: Understand that patterns of association can also be seen in bivariate categorical data by displaying frequencies and relative frequencies in a two-way table. Construct and interpret a two-way table summarizing data on two categorical variables collected from the same subjects. Use relative frequencies calculated for rows or columns to describe possible association between the two variables. For example, collect data from students in your class on whether or not they have a curfew on school nights and whether or not they have assigned chores at home. Is there evidence that those who have a curfew also tend to have chores?Standards for Mathematical Practice Emphasized:
1. Make sense of problems and persevere in solving them.
2. Reason abstractly and quantitatively.
3. Construct viable arguments and critique the reasoning of others.
4. Model with mathematics.
5. Use appropriate tools strategically.
6. Attend to precision.
7. Look for and make use of structure.
8. Look for and express regularity in repeated reasoning.
Instructional Notes:
This lesson is a summary lesson in which the students use their knowledge of probability to make informed decisions. The students will use unions, intersections and complements to compute and interpret theoretical and experimental probabilities of compound events, attending to mutually exclusive events, independent events and conditional probabilities. While this lesson is independent of the prior lessons of this module as well as previous modules, it is a culminating lesson. In a sense, this lesson can be considered a “great mathematical task” that can be used to assess student learning of the Common Core Algebra 2 probability and statistics standards. If you find the students are struggling to complete the Reflection portion of this lesson, provide them with the Charity Fair mathematics task found in the Mathematics Assessment Project 
, Apprentice Task A01.
Because of the culminating nature of this lesson, it may behoove you to reread Progressions for the Common Core State Standards in Mathematics . These documents provide an overview of conditional probability, providing real-world applications as well as simulations and two-way table examples. The examples provided in these documents can be used as an assessment for learning as students work through the lesson.
> Go to Prize Winner, Part 3 lesson
Sample Responses
For sample responses to the Algebra II Journal questions, visit the Algebra II Journal in the Teacher Resources.
Prize Winner, Part 3 - Page 1
If students are having difficulty applying the probability formulas, encourage them to construct a tree diagram to map out all the different combinations of doors. For example,
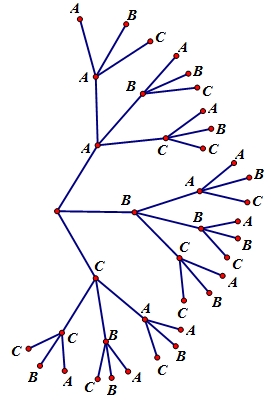
Prize Winner, Part 3 - Page 2
A tree diagram may be helpful here as well. Also, suggest to the students that they create a tactile version of the game using index cards. Understanding the contextual meaning of the probabilities is just as important, if not more important, than just the ability to apply the probability formulas.
UDL Opportunities:
Principle 1: Provide Multiple Means of Representation
Checkpoint 1.1 Offer ways of customizing the display of information.
Checkpoint 1.3 Offer alternatives for visual information.
Checkpoint 2.1 Clarify vocabulary and symbols.
Checkpoint 2.2 Clarify syntax and structure.
Checkpoint 2.3 Support decoding text, mathematical notation, and symbols.
Checkpoint 3.1 Activate or supply background knowledge.
Checkpoint 3.2 Highlight patterns, critical features, big ideas, and relationships.
Checkpoint 3.4 Maximize transfer and generalization.
Principle 2: Provide Multiple Means of Action and Expression
Checkpoint 4.2 Optimize access to tools and assistive technologies.
Checkpoint 5.3 Build fluencies with graduated levels of support for practice and performance.
Checkpoint 6.2 Support planning and strategy development.
Checkpoint 6.3 Facilitate managing information and resources.
Checkpoint 6.4 Enhance capacity for monitoring progress.
Principle 3: Provide Multiple Means of Engagement
Checkpoint 7.2 Optimize relevance, value, and authenticity.
Checkpoint 7.3 Minimize threats and distractions.
Checkpoint 8.4 Increase mastery-oriented feedback.
Checkpoint 9.1 Promote expectations and beliefs that optimize motivation.
Checkpoint 9.3 Develop self-assessment and reflection.
