Prize Winner, Part 2
Estimated Time: 45 minutes
Lesson Objectives:
- The students will determine the conditional probabilities given a two-way table.
- The students will determine if two conditional events are independent or dependent.
Resources for this lesson:
Before you begin, download your Algebra II Journal 
for Prize Winner, Part 2. You will be completing activities in the journal throughout this lesson.
Visit this section on each page to access information about key terms and other resources to help facilitate the lesson.
> Glossary
> Calculator Resources
> Teacher Resources: Instructional Notes
Key Common Core State Standards:
S.CP.3: Understand the conditional probability of A given B as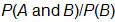
, and interpret independence of A and B as saying that the conditional probability of A given B is the same as the probability of A, and the conditional probability of B given A is the same as the probability of B.
S.CP.4: Construct and interpret two-way frequency tables of data when two categories are associated with each object being classified. Use the two-way table as a sample space to decide if events are independent and to approximate conditional probabilities. For example, collect data from a random sample of students in your school on their favorite subject among math, science, and English. Estimate the probability that a randomly selected student from your school will favor science given that the student is in tenth grade. Do the same for other subjects and compare the results.
S.CP.5: Recognize and explain the concepts of conditional probability and independence in everyday language and everyday situations. For example, compare the chance of having lung cancer if you are a smoker with the chance of being a smoker if you have lung cancer.
S.CP.6: Find the conditional probability of A given B as the fraction of B’s outcomes that also belong to A, and interpret the answer in terms of the model.Supporting Common Core State Standards:
7.SP.C.8: Find probabilities of compound events using organized lists, tables, tree diagrams, and simulation.
7.SP.C.8a: Understand that, just as with simple events, the probability of a compound event is the fraction of outcomes in the sample space for which the compound event occurs.
7.SP.C.8b: Represent sample spaces for compound events using methods such as organized lists, tables and tree diagrams. For an event described in everyday language (e.g., “rolling double sixes”), identify the outcomes in the sample space which compose the event.
8.SP.4: Understand that patterns of association can also be seen in bivariate categorical data by displaying frequencies and relative frequencies in a two-way table. Construct and interpret a two-way table summarizing data on two categorical variables collected from the same subjects. Use relative frequencies calculated for rows or columns to describe possible association between the two variables. For example, collect data from students in your class on whether or not they have a curfew on school nights and whether or not they have assigned chores at home. Is there evidence that those who have a curfew also tend to have chores?
S.CP.1: Describe events as subsets of a sample space (the set of outcomes) using characteristics (or categories) of the outcomes, or as unions, intersections, or complements of other events (“or”, “and”, “not”).Standards for Mathematical Practices:
1. Make sense of problems and persevere in solving them.
2. Reason abstractly and quantitatively.
3. Construct viable arguments and critique the reasoning of others.
4. Model with mathematics.
5. Use appropriate tools strategically.
6. Attend to precision.
7. Look for and make use of structure.
8. Look for and express regularity in repeated reasoning.
