Fan Appreciation Night, Part 2
Resources for this lesson:
Key Terms:
Intersection
Union
Addition Rule
> Glossary 
> Calculator Resources
> Teacher Resources: Instructional Notes
Create and Analyze
The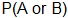 
is known as finding the probability of the intersection of A and B, and may also be written as 
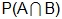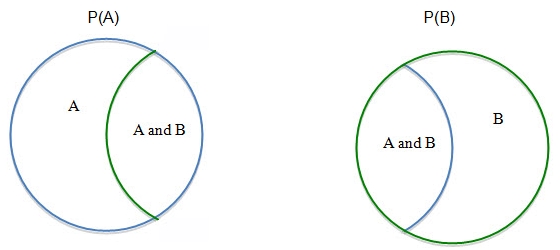
. Let’s explore what finding 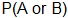means for mutually inclusive events. Since mutually inclusive events can occur at the same time, the situation can be represented with a Venn diagram:
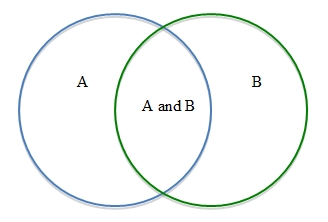
To find the probability of the intersection of A or B, 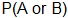, we cannot simply find the 
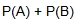, because the two probabilities overlap with the section 
. This section would be counted twice.
Since the , the union of A and B, is counted twice, you would need to subtract one of these sections to find the 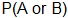. So, when events are mutually inclusive, you apply the Addition Rule,
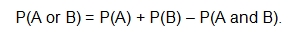
Let’s explore how to find the probability of winning a t-shirt or a hat.
for mutually inclusive events, add the probability of the first event to the probability of the second event and then subtract the probability of both occurring. 