Prize Winner, Part 1
 Resources for this lesson:
Resources for this lesson:
![]() Key Terms:
Key Terms:
Experimental probability
> Glossary ![]()
> Calculator Resources ![]()
> Teacher Resources: Instructional Notes ![]()
Andrew thinks the game is too easy, and suggests ways to make the game more challenging. Justyce says that there should be three levels of prizes: small, medium and large, with new rules for winning. The group agrees.
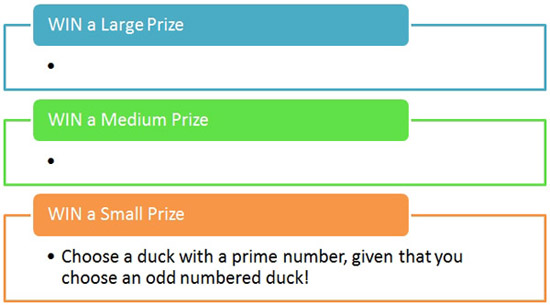
 Andrew: “What if we changed the rules so that in order to win a small prize, a person playing the game must select a duck that has a prime number painted on the bottom?”
Andrew: “What if we changed the rules so that in order to win a small prize, a person playing the game must select a duck that has a prime number painted on the bottom?”
Khalid starts designing a “Rules of the Game” sign. On it, he writes the following:
 Real-Life Scenarios
Real-Life Scenarios
> Text version for animation
 Check Your Understanding
Check Your Understanding
 Check Your Understanding
Check Your Understanding
You may be wondering what the difference is between having the rule for a small prize state:
- “What is the probability of a person selecting a prime and odd number?”
versus:
- “What is the probabilty of a person selecting a prime number, given that they selected an odd number?”
You already know the answer to (a) is. This probability is referring to all of the numbers that are odd and prime out of all thirty numbers. In the Venn Diagram, these are the nine numbers that appear in the center out of all thirty numbers.
You also already know from Andrew’s explanation, the answer to (b) is . We can also see this in the Venn Diagram. Given that the gamer chooses an odd number first, we are limited to the 15 odd numbers. From this circle, we choose the prime numbers. Thus, we get 9 prime numbers out of the 15 odd numbers, or . This simplifies to the Andrew got.


