Prize Winner, Part 1

Home > Prize Winner, Part 1 > Page 6

You do not need to draw a Venn Diagram or list numbers every time you want to calculate conditional probability. Let’s develop a formula for conditional probability.

Recall that the last example wanted us to find the probabilty of a person selecting a multiple of five, given that they selected an even number. We found this probability to be${\displaystyle \frac{1}{5}}$.

Using probability notation, this would be 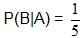, where:

B: the event of “selecting a multiple of five”

A: the event of “selecting an even number”

The “given that” condition limits the number of elements we can choose from. “Given that they select an even number” involves the probability that an even number is chosen. This is 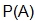. In this example, that is ${\displaystyle \frac{15}{30}=\frac{1}{2}}$

The “selecting a multiple of five” event is not just , or 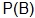. It is not this because we can only select a multiple of five from the even number set. This is , the probability of selecting a number that is a multiple of five and is an even number. In this example, that is ${\displaystyle \frac{3}{30}}$, or ${\displaystyle \frac{1}{10}}$. (A word of caution here. Do not jump to using the Multiplication Rule, 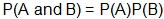, which is only for independent events. More on this later.)

Now, consider the way that 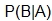is read. It is read “the probability of B given A.” Because of the condition of the situation, the probability of B is really from the reasoning above. The “given A” is 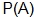, from above. Thus,

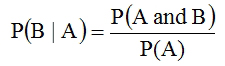
Checking with the example above, .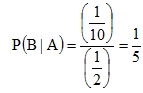

 

< Previous Next >