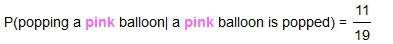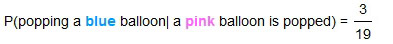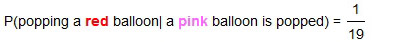Prize Winner, Part 1

Home > Prize Winner, Part 1 > Page 9

Therefore, to summarize that last exercise, we know:

In order to win a prize, a gamer must pop a pink balloon first. Thus, the second step is dependent on the first. The events are dependent. This means 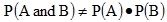and therefore 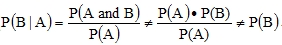. The events A and B, that is popping a pink and then a green, are dependent on each other.

It may seem that the games that Khalid, Justyce, Andrew, Marissa and Allyson are developing have a relatively high probability of winning. For example, if we want to win a small prize, we have to pop a green balloon after popping a pink one. From above, we know that 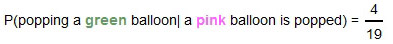, which is a 21% chance.

Be careful to interpret conditional probabilities correctly. This 21% chance is the chance of winning after a pink balloon is popped. This is not the probability of winning overall.

To find the probability of winning, follow these steps:

• The probability of a pink balloon being popped first is ${\displaystyle \frac{12}{20}}$.
• Then, the probability of popping a green balloon given the pink balloon is popped first  is ${\displaystyle \frac{4}{19}}$.
• The probability of both of these events happening is ${\displaystyle \left(\frac{12}{20}\right)\left(\frac{4}{19}\right)=0.126}$.

There is a 12.6% chance of winning a small prize.

< Previous Next >