Prize Winner, Part 2

Home > Prize Winner, Part 2 > Page 4

As Khalid, Justyce, Andrew, Marissa and Allyson set up the games, they wonder how many children they could expect to show for the carnival.

Khalid collects data for their community comparing the age of the head of household to the number of children in the household.

Analysis of Number of Children Living in the Household compared to the

Age of the Head of the Household

Check Your Understanding

Is the number of children living in a household in this community independent or dependent of the age of the head of the household? If the answer to this question is that the events are independent, then.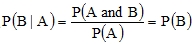

Let’s check the above exercise, 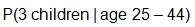. 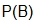would be . According to the table, the probability of having three children in a household is ${\displaystyle \frac{380}{8947}}$. This is not equal to the value we found for 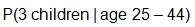. Thus, the number of children in a household is dependent on the age of the head of the household.

In mathematics, it is never good to draw such a conclusion off of one example. Try another.

Check Your Understanding

Based on the last two exercises, is the number of children living in a household  independent or dependent of the age of the head of the household?

Remember, the conditional probability  is generally not equal to the probability P(B). This is because the Event A gives us information about whether or not Event B occurs. For this last example, knowing the age of the head of the household (Event A) gives us information about whether or not there are likely to be children living in the household (Event B).

< Previous Next >