Fan Appreciation Night, Part 1

Home > Fan Appreciation Night, Part 1 > Page 6

Since the events in this scenario are dependent, a different strategy must be applied to calculate the probability.

Create and Analyze

One way to look at this scenario is by creating a sample space.  Each letter in the sample space represents a different category of question that may be drawn.  Let’s say the cards with the letter H are the history cards.

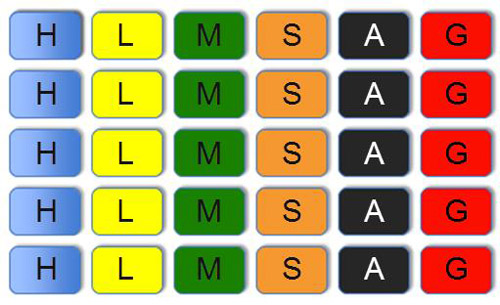
The probability of drawing a history card first is ${\displaystyle \frac{5}{30}}$ or ${\displaystyle \frac{1}{6}}$.

If one history card is drawn first, the sample space for the drawing of the second question would look like this:

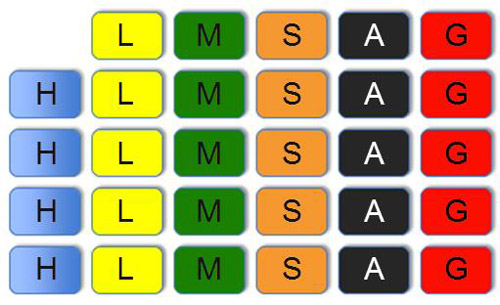
The sample space has now changed, indicating that this event is dependent and the probability of the second draw being a history card is now${\displaystyle \frac{4}{29}}$.  If the events were independent, the sample space would not change, such as in cases where cards are replaced in the pile.

To calculate the probability of dependent events, you must multiply the probability of event A with the probability of B after A occurs.

Test and Confirm

So, the probability of drawing the first history card is${\displaystyle \frac{5}{30}}$ or ${\displaystyle \frac{1}{6}}$.  Once that card is selected, there are only 29 cards remaining and only 4 of those cards represent history questions.  The probability of drawing a second history card is ${\displaystyle \frac{4}{29}}$.  So, the probability of drawing two history questions is ${\displaystyle \left(\frac{1}{6}\right)\left(\frac{4}{29}\right)=\frac{2}{87}}$ . 

Apply the Model

It would not be likely that two history questions would be drawn in a row.

 

< Previous Next >