Just How Normal Are You?

Home > Just How Normal Are You? > Page 7

Andrew and Khalid are discussing what they have learned so far about the presidents.

The table below displays the weights of the presidents.

President	Weight (pounds)
1. G. Washington	175
2. J. Adams	150
3. T. Jefferson	174
4. J. Madison	100
5. J. Monroe	189
6. J. Q. Adams	174
7. A. Jackson	140
8. M. Van Buren	173
9. W. H. Harrison	139
10. J. Tyler	141
11. J. Polk	174
12. Z. Taylor	170
13. M. Fillmore	164
14. F. Pierce	144
15. J. Buchanan	198
16. A. Lincoln	180
17. A. Johnson	174
18. U. Grant	156
19. R. Hayes	170
20. J. Garfield	184
21. C. Arthur	224
22. G. Cleveland	260
23. B. Harrison	150
24. G. Cleveland	260
25. W. McKinley	199
26. T. Roosevelt	210
27. W. H. Taft	316
28. W. Wilson	170
29. W. Harding	173
30. C. Coolidge	147
31. H. Hoover	187
32. F. D. Roosevelt	188
33. H. Truman	167
34. D. Eisenhower	171
35. J. F. Kennedy	173
36. L. Johnson	200
37. R. Nixon	175
38. G. Ford	190
39. J. Carter	160
40. R. Reagan	185
41. G. H. Bush	196
42. W. Clinton	223
43. G. W. Bush	191
44. B. Obama	180

Check Your Understanding

Use the graphing calculator to construct a histogram of the data. Shown below is a suggested WINDOW to use for graphing the histogram in the calculator. Remember to use President Cleveland’s weight only once.

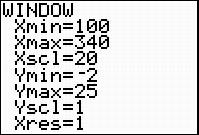
Check Your Understanding

Show AnswerHide Answer

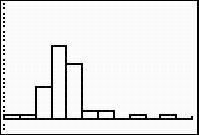
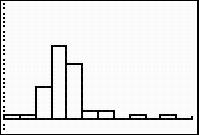A histogram of the Weights of the Presidents is shown. The x axis is labeled Weights of Presidents, and it is numbered from 135 to 270, counting in increments of 5. The y axis is labeled Frequency and is numbered from zero to 8 counting in increments of 1. The histogram is skewed left, with the highest bar between 165 and 175. The highest bar reaches a frequency of 6. There is a gap between 225 and 260.

Use the mean and standard deviation you calculated to sketch the normal curve for this normal distribution. (You may use the features of the graphing calculator to construct a normal distribution for this data if you feel comfortable with the calculator’s features. Be sure to adjust your window appropriately.)

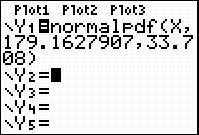
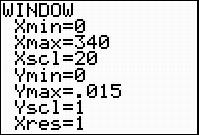
Check Your Understanding

Show AnswerHide Answer

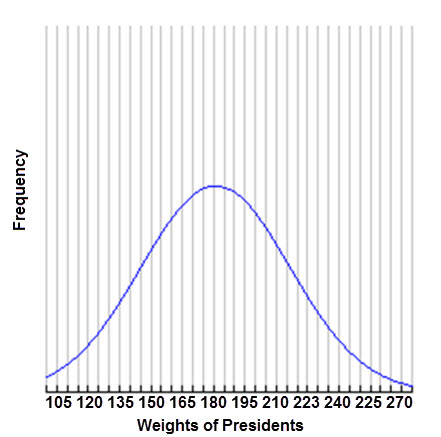A bell shaped normal curve is shown. The x axis extends from 105 to 270, with the peak of the bell at 180. The x axis is labeled Weights of Presidents and the y axis is labeled Frequency.

Compare and contrast the normal distribution with the histogram.

President’s Weights	Normal Distribution

What do you notice?

You should notice that the weights are most definitely not normally distributed! The weights of the heavier presidents, such as President Taft, skew the data to the right.

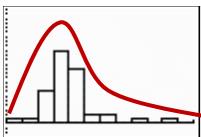
This data set is a reminder: While many data sets follow a normal distribution, many do not! As you continue your work with data distributions, mean and standard deviation, remember this important fact. Normal distributions are special, and not all data sets are normal.

Algebra II Journal: Reflection 3

In this lesson, you used the mean and standard deviation of a data set to fit the data to a normal distribution and to estimate percentages using the normal distribution.

Respond to the following reflection questions in your Algebra II Journal and submit to your teacher.

 

< Previous > Go to Home Page
> Go to next lesson: X…Y…Zzzzzzz