Skip to section navigation Skip to main content

Plinko

Home > Plinko > Page 4

Resources for this lesson:

Key Terms

Normal Distribution

> Glossary opens in new window
> Calculator Resources opens in new window
> Teacher Resources: Instructional Notes opens in new window

This is a bar graph displaying the frequency of the presidents’ ages at inauguration. The horizontal axis is labeled ‘Presidents’ Ages at Inauguration’, and extends from 36 to 76. The vertical axis is labeled ‘Frequency’ and extends from 0 to 10. The first bar covers the age range 42 to 44 years and has a frequency of 2. The next bar covers the range of 46 to 48 years and has a frequency of 4. The next bar covers the range 48 to 50 years and has a frequency of 3. The next bar covers the range 50 to 52 years and has a frequency of 6. The next bar covers the range 52 to 54 years and has a frequency of 2. The next bar covers the range 54 to 56 years and has a frequency of 9. The next bar covers the range 56 to 58 years and has a frequency of 7. The next bar covers the range 58 to 60 years and has a frequency of 1. The next bar covers the range 60 to 62 years and has a frequency of 4. The next bar covers the range 62 to 64 years and has a frequency of 1. The next bar covers the range 64 to 66 years and has a frequency of 3. The last bar covers the range 68 to 70 years and has a frequency of 2.

The Presidents’ Ages histogram is a normal distribution. The normal curve drawn above the distribution is single peaked. It is symmetric about that peak and has a bell shape.

Return to the presidents’ ages at inauguration.

Presidents' AgesHide Answer

 

Check Your Understanding

Because the data is representing the entire population of presidents, the symbol μ (“mu”) is used to represent the mean, instead of (x). A lower case "m" from the  Greek alphabet is represented by the symbol μ. This symbol is used for the mean when the data for an entire population is used Thus, you found the mean for the presidents’ ages to be μ = 54.659.

Notice that the arrow that points to the mean also points to the peak of the normal curve.

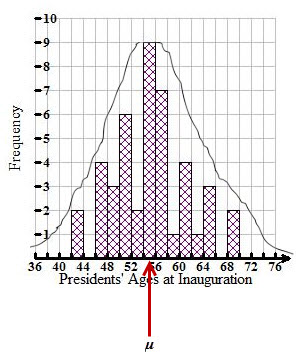
The same bar graph. A curve is drawn above the bars of the bar graph showing the trend of the graphs. The curve starts at point 36, 0.5 and rises to the maximum point 56, 9 and then decreases to 76, 0.5. An arrow labeled mu points to the mean at age 54.549.

You should further notice that approximately half of the bars (half of the data) fall below the mean, and half of the bars (half of the data) falls above the mean. This is what is meant by the curve being symmetric. This is an important characteristic of a normal curve.

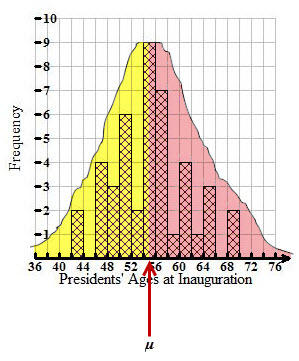
The same bar graph. A curve is drawn above the bars of the bar graph showing the trend of the graphs. The curve starts at point 36, 0.5 and rises to the maximum point 56, 9 and then decreases to 76, 0.5. An arrow labeled mu points to the mean at age 54.549. The data below the mean is shaded yellow and the data above the mean is shaded pink.


In a perfect normal distribution, the mean is exactly in the middle of the data. In a perfect normal distribution, exactly half the data falls below the mean, and exactly half the data falls above the mean. (The mean and the median are exactly equal.)

 

< Previous Next >