Plinko
Resources for this lesson:
You will use your Algebra II Journal 
on this page.
> Glossary
> Calculator Resources
> Teacher Resources: Instructional Notes
It’s time to try another example.
Listed below are the ages for the vice presidents of the United States.
Vice President |
Age at Inauguration |
|---|---|
1. J. Adams |
53 |
2. Jefferson |
53 |
3. Burr |
45 |
4. G. H. Clinton |
65 |
5. Gerry |
68 |
6. Tompkins |
42 |
7. Calhoun |
42 |
8. Van Buren |
50 |
9. R. M. Johnson |
56 |
10. Tyler |
50 |
11. Dallas |
52 |
12. Fillmore |
49 |
13. King |
66 |
14. Breckinridge |
36 |
15. Hamlin |
51 |
16. A. Johnson |
56 |
17. Colfax |
45 |
18. Wilson |
61 |
19. Wheeler |
57 |
20. Arthur |
51 |
21. Hendricks |
65 |
22. Morton |
64 |
23. Stevenson |
57 |
24. Hobart |
52 |
25. T. Roosevelt |
42 |
26. Fairbanks |
52 |
27. Sherman |
53 |
28. Marshall |
58 |
29. Coolidge |
48 |
30. Dawes |
59 |
31. Curtis |
69 |
32. Garner |
64 |
33. Wallace |
52 |
34. Truman |
60 |
35. Barkley |
71 |
36. Nixon |
40 |
37. L. B. Johnson |
52 |
38. Humphrey |
53 |
39. Agnew |
50 |
40. Ford |
60 |
41. Rockefeller |
66 |
42. Mondale |
49 |
43. G. H. Bush |
56 |
44. Quayle |
41 |
45. Gore |
44 |
46. Cheney |
59 |
47. Biden |
66 |
Algebra II Journal: Reflection 2
Respond to the following reflection questions in your Algebra II Journal and submit to your teacher.
- Construct a histogram for the Vice Presidents of the United States data.
- Use what you know about mean (μ) and standard deviation (
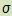)and data distributions to justify why the ages of the vice presidents form a normal distribution. - What percentage of the ages is within one standard deviation of the mean (−1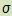and +1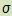)? What is this range of ages?
- How close does the data fit the 95.44% rule, where 95.44% of the data falls within two standard deviations of the mean (μ ± 2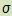)? How close does the data fit the 99.74% rule, where 99.74% of the data falls within three standard deviations of the mean (μ ± 3)?
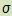