Prize Winner, Part 1
Resources for this lesson:
Key Term
Conditional Probability
> Glossary 
> Calculator Resources
> Teacher Resources: Instructional Notes
Again, you might be wondering what the difference is between the rule stating:
- “What is the probability of a person selecting an even number and a multiple of five?”
versus:
- “What is the probabilty of a person selecting a multiple of five, given that they selected an even number?”
A Venn Diagram makes this very clear.
Check Your Understanding
Finding the probability of a person selecting an even number and a multiple of five means that we look at all the numbers 1 – 30, and select the numbers that are both even and a multiple of five. Three out of the thirty numbers fit this description, so the probability is .
Finding the probabilty of a person selecting a multiple of five, given that they already selected an even number means that the person must begin with selecting the even number first. This limits us to just the fifteen even numbers. From that set, we then look for the multiples of five, which are 10, 20 and 30. Thus, the probabiltiy is .
Check Your Understanding
It is important to note that this does not mean the chance of winning a medium prize is 50%. It means that, under the condition that a duck with a multiple of five is chosen, there is a 50% chance of that number being even.
This probability is called conditional probabilityconditional probability. The following notation is used for conditional probability:
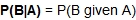= the probability of event B happening given that event A happens
