Skip to section navigation Skip to main content

Exploring Other Function Models

Home > Exploring Other Function Models > Page 11

Resources for this lesson:

> Glossary opens in new window
> Calculator Resources opens in new window
> Teacher Resources: Instructional Notes opens in new window

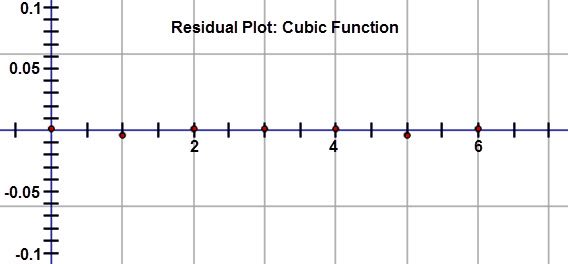
This graph is a residual plot displaying the residuals for the Natural Gasoline Prices when a cubic regression equation is applied to the data. The graph is titled, ‘Residual Plot: Cubic Function.’ The horizontal axis represents the months and extends from negative 0.5 to 7. The vertical axis represents the residual values and extends from negative 0.1 to 0.1. The graph displays the following ordered pairs: (0, 0.001), (1, negative 0.004), (2, 0.001), (3, 0.001), (4, 0.001), (5, negative 0.004), and (6, 0.001).

After inspecting the residuals, Khalid notices that the residuals are very close to zero and do not show a pattern.  So, a cubic regression is an excellent fit for the data set. 

Just to be sure, he decides to calculate a quartic regression.  Here is the quartic regression equation:

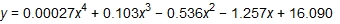
y equals 27 hundred-thousandths x to the fourth power plus 103 thousandths x cubed minus 536 thousandths x squared minus 1 and 257 thousandths x plus 16 and 90 thousandths

kahlid holding a calculator and speakingKhalid: For this regression equation, the leading coefficient is close to 0.  When this happens for a polynomial function, it indicates that the best fit is one degree less.  So, the cubic function is in fact the best fit for the data.


 


< Previous Next >