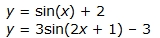Exploring Other Function Models
Resources for this lesson:
Key Term
Periodic
> Glossary 
> Calculator Resources
> Teacher Resources: Instructional Notes
Test and Confirm
Since the residual plot revealed a potential pattern, Khalid will need to consider other function families.
Check Your Understanding
Function Families
Each of the function families listed below can be used to calculate a regression equation. Select a function family to learn more.
Cubic Functions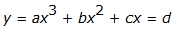
Graph may have no maximum/minimum values, or exactly one maximum and one minimum value.
Some sample cubic functions could include: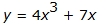
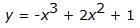
Volume data would typically be modeled with a cubic function.
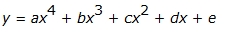
Graphs have either:
1 maximum/minimum value
or
2 maximum values and 1 minimum value
or
2 minimum values and 1 maximum value
Some sample quartic functions include:
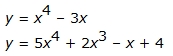
This function family is not as common a fit for data, but should still be considered.
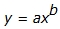
This function family includes some functions that also belong to other function families. Any function that can be written as a number times x raised to a power (where the power is any real number) is considered a member of the power function family. Some samples of power functions include:
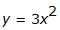(Quadratic function)
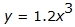(Cubic function)
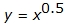(Square root function/Radical function)
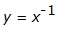(Inverse function/Rational function)
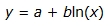
Graphs are either always increasing or always decreasing. There are no maximum or minimum values.
The graph has a horizontal asymptote.
The form of the logarithmic equation uses the natural base e. Logarithmic functions could have any base. Any logarithmic function can be represented as a function with the natural base.
Some sample natural logarithmic functions include:
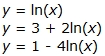
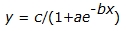
Graph is an S-shaped curve.
A sample logistic function could be:
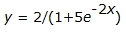
The spread of a disease data typically can be modeled with a logistic curve.
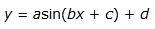
Trigonometric functions are periodic (a function that repeats values in regular intervals). There are six main trigonometric functions.
Real world data that is periodic in nature is typically modeled by the sine function. Average daily temperatures in a given city or the height of the water in the bay during a 24-hour period are real world situations which may produce data that could be modeled by the sine function.
Sample sinusoidal functions include:
